Question

Center is (2,-2) another point on the circle is (-4,6) An equation of the circle in standard form is what?

Answer 1

(x - 2)^2 + (y + 2)^2 = 100

Explanation:

We know that the equation for a circle with a center in the point (a, b) and a radius R is given by:

(x - a)^2 + (y - b)^2 = R^2

Here we know that the center of the circle is the point (2, - 2) and that the point (-4, 6) lies on the circle.

Then the radius of this circle will be the distance between (2, - 2) and (-4, 6)

Remember that the distance between two points (x₁, y₁) and (x₂, y₂) is given by:

`D = √((x_1 - x_2)^2 + (y_1 - y_2)^2)`

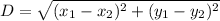
Then the distance between (2, - 2) and (-4, 6) is:

`D = √((2 - (-4))^2 + (-2 - 6)^2) = √(6^2 + (-8)^2) = √(100) = 10`

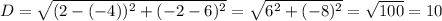
Then the radius of the circle is R = 10

and we know that the center is (2, -2)

the equation for this circle is then:

(x - 2)^2 + (y - (-2))^2 = 10^2

(x - 2)^2 + (y + 2)^2 = 100