Answer:
A directly proportionality between x and y is written as:
y = k*x
where k is the constant of proportionality.
Then, if p is directly proportional to (q + p)^2
We can write this as:
p = k*(q + p)^2
Now we know that q = 1 when p = 1
Then we can replace these values in the above equation to find the value of k
1 = k*(1 + 1)^2
1 = k*2^2 = k*4
1/4 = k
Then the equation is:
p = (1/4)(p + q)^2
Now we want to find the value of q when p = 10
So we just replace p by 10, and solve the equation
10 = (1/4)*(q + 10)^2
10*4 = (q + 10)^2
40 = q^2 + 2*q*10 + 10^2
40 = q^2 + 20*q + 100
This is a quadratic equation for q, such that:
q^2 + 20*q + 100 - 40 = 0
q^2 +20*q + 60 = 0
This is the equation that gives the value of q when p = 10
To solve this, we can use Bhaskara's equation, which says that for a quadratic equation:
a*x^2 + b*x + c = 0
The solutions are given by:
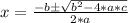
In this case, the solutions for q are:
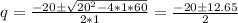
Then we have two possible values for q:
q = (-20 + 12.65)/2 = -3.675
q = (-20 - 12.65)/2 = -16.325