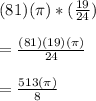Answer:
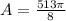
Explanation:
1.Approach
To solve this problem, find the total area of the circle. Then multiply the total area by the fraction of the circle that is shaded.
2.Find the area of the circle
The formula to find the area of a circle is the following,
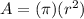
Where (
 ) represents the radius of the circle, that is the distance from the center of the circle to the circumference of the circle (the outer edge). (
) represents the radius of the circle, that is the distance from the center of the circle to the circumference of the circle (the outer edge). (
 ) represents the numerical value (3.1415..).
) represents the numerical value (3.1415..).
Substitute the given values into the formula and solve for the area.
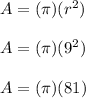
3.Find the percent of the circle that is shaded
There are a total of (360) degrees in a circle. It is given that (75) degrees are not shaded. To find the fraction of a circle that is shaded, subtract (75) form (360). Then put this value over (360) and simplify.
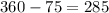
Now put this number over (360) to find the fraction of the circle that is shaded.
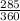

4.Find the area of the shaded region
Now multiply the total area by the fraction that the shaded region occupies.