Question

A 16 kg science book is dropped of a 120 meter high cliff. Assuming a closed system:

a) how fast is book traveling the instant before it impacts the ground below the cliff?
b) how far above the bottom of the cliff is the object moving at 12 m/s?

Answer 1

Step-by-step explanation:

The mass of that science book...wow. In pounds that would be 35.2! Yikes!

Anyway, we need final velocity here, and the mass of the book has nothing to do with how fast it falls. Everything is pulled by the same gravity. A feather falls at 9.8 m/s/s and so does an elephant. Mass is useless information. The equation we will use is

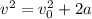`v^2=v_0^2+2a`Δx where

v is the final velocity, our unknown,

v₀ is the initial velocity which is 0 since someone had to be holding the book before dropping it,

a is the pull of gravity which is always -9.8 m/s/s, and

Δx = -120 which is the displacement (it's negative because the book falls below the point from which it was dropped). Filling in:

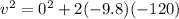`v^2=0^2+2(-9.8)(-120)` so

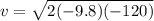`v=√(2(-9.8)(-120))` and

v = 48 m/s

As far as how far above the bottom of the cliff the object is when it is moving at 12 m/s we will use the same equation, but the velocity will be 12:

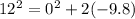`12^2=0^2+2(-9.8)`Δx and

144 = -19.6Δx so

Δx = -7.3 m. That's how far from the top of the cliff it is. We subtract then t find out how far it is from the bottom:

120 - 7.3 = 112.7 m off the ground.