Answer:
The absolute maximum and the absolute minimum are (0, 16) and (2, 0).
Explanation:
First, we obtain the first and second derivatives of the function by chain rule and derivative for a power function, that is:
First derivative
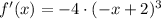
Second derivative
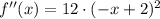
Then, we proceed to do the First and Second Derivative Tests:
First Derivative Test
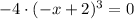
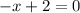
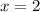
Second Derivative Test
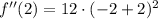

The Second Derivative Test is unable to determine the nature of the critical values.
Then, we plot the function with the help of a graphing tool. The absolute maximum and the absolute minimum are (0, 16) and (2, 0).