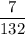Question

Suppose a jar contains 8 red marbles and 25 blue marbles. If you reach in the jar and pull out 2 marbles at random, find the probability that both are red.

Answer 1

Answer:
`(7)/(132)`

Explanation:

Total marbles in the jar = 8+25 = 33

Using combinations, the number of ways of choosing two marbles out of 33=
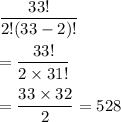`(33!)/(2!(33-2)!)\\\\=(33!)/(2*31!)\\\\=(33*32)/(2)=528` (total outcomes)

Similarly, the number of ways of choosing two red marbles =

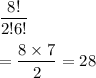`(8!)/(2!6!)\\\\=(8*7)/(2)=28`(favorable outcomes)

Required probability =
`\frac{\text{favorable outcomes}}{\text{total outcomes}}`

`=(28)/(528)\\\\=(7)/(132)`

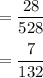
hence, required probability =
`(7)/(132)`