Question

Let f be a function of two variables that has continuous partial derivatives and consider the points

A(8, 9),

B(10, 9),

C(8, 10),

and

D(11, 13).

The directional derivative of f at A in the direction of the vector AB is 9 and the directional derivative at A in the direction of

AC is 2. Find the directional derivative of f at A in the direction of the vector AD.

(Round your answer to two decimal places.)

Answer 1

The directional derivative of f at A in the direction of
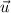`\vec{u}` AD is 7.

Explanation:

Step 1:

Directional of a function f in direction of the unit vector
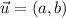`\vec{u}=(a,b)` is denoted by
`D\vec{u}f(x,y)`,

`D\vec{u}f(x,y)=f_(x)\left ( x ,y\right ).a+f_(y)(x,y).b`.

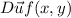Now the given points are

`A(8,9),B(10,9),C(8,10) and D(11,13)`,

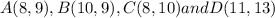Step 2:

The vectors are given as

AB = (10-8, 9-9),the direction is

`\vec{u}_(AB) = (AB)/(\left \| AB \right \|)=(1,0)`

AC=(8-8,10-9), the direction is

`\vec{u}_(AC) = (AC)/(\left \| AC \right \|)=(0,1)`

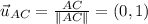
AC=(11-8,13-9), the direction is

`\vec{u}_(AD) = (AD)/(\left \| AD \right \|)=\left ((3)/(5),(4)/(5) \right )`

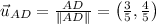
Step 3:

The given directional derivative of f at A
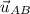`\vec{u}_(AB)` is 9,

`D\vec{u}_(AB)f=f_(x) \cdot 1 + f_(y)\cdot 0\\f_(x) =9`

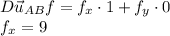
The given directional derivative of f at A
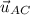`\vec{u}_(AC)` is 2,

`D\vec{u}_(AB)f=f_(x) \cdot 0 + f_(y)\cdot 1\\f_(y) =2`

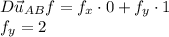
The given directional derivative of f at A
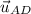`\vec{u}_(AD)` is

`D\vec{u}_(AD)f=f_(x) \cdot (3)/(5) + f_(y)\cdot (4)/(5)`

`D\vec{u}_(AD)f=9 \cdot (3)/(5) + 2\cdot (4)/(5)`

`D\vec{u}_(AD)f= (27+8)/(5) =7`

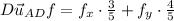
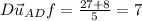
The directional derivative of f at A in the direction of
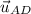`\vec{u}_(AD)` is 7.