Solution :
According to the theory of demand and supply, the equilibrium price and the quantity is established where both the demand and supply curves intersect.
From the graph, we can see that the point of equilibrium is at the intersection of D and S.
At this point, mathematically, D = S. In order to determine the price and quantity which exists at this point, we need to equate the demand as well as supply functions to calculate the equilibrium values.
∵ D is equal to S, we have
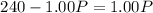
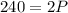
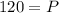
Now substituting this value of the equilibrium price in to any of the functions, we get the equilibrium quantity at this price.
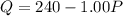
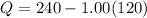

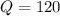
This is the equilibrium quantity. At this point, equilibrium price as well as the quantity is the same. Let the price of the golf club increases from $120 to $140. So substituting the value to the function above to determine the new quantity.

= 100
Therefore, when the demanded quantity decreases from 120 thousand clubs to 100 thousand clubs. This increases the price and decreases the quantity as the supply curve moved to the left. The demand remains constant.