Question

Mercury Company has only one inventory pool. On December 31, 2021, Mercury adopted the dollar-value LIFO inventory method. The inventory on that date using the dollar-value LIFO method was $201,000. Inventory data are as follows:

Year Ending Inventory at Year-End Costs Ending Inventory at Base Year Costs
2019 $260,400 $248,000
2020 347,300 302,000
2021 350,400 292,000

Required:
Compute the inventory at December 31, 2019, 2020, and 2021, using the dollar-value LIFO method.

Answer 1

Step-by-step explanation:

The cost index can be calculated as follows:

In 2019:

= 260400/248000

= 1.05

In 2020:

= 347300/302000

= 1.15

In 2021:

= 350400/292000

= 1.2

Inventory Layers converted to the base cost

Date
`\text{(Inventory at } \ \ \ \ \ \ \ \ \text{(year-end } \\ \\ \text{ year end cost) } / \ \ \ \text{cost index) } = \ \ \ \ \ \ \ \text{ Inventory layers(base year cost) }`

12/31/20 201000 ÷ 1 = 201000

12/31/20 260400 ÷ 1.05 = 248000

12/31/20 347300 ÷ 1.15 = 302000

12/31/20 350400 ÷ 1.2 = 292000

Inventory Layers converted to cost Ending Inventory DVL cost

`\text{(Inventory layers } \ \ \text{(`

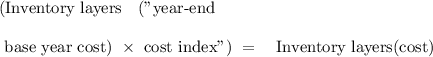
Base

201000 × 1 = 201000

201000 × 1 = 201000

Dec 31, 2019

47000 × 1.05 = 49350

ADD 250350

Base

201000 × 1 = 201000

Dec 31, 2019

47000 × 1.05 = 49350

Dec 31, 2020

(302000 - 248000)

= 54000 × 1.15 = 62100

ADD 312450

Base

201000 × 1 = 201000

Dec 31, 2019

47000 × 1.05 = 49350

Dec 31, 2021

(292000 - 248000)

= 44000 × 1.15 = 50600

ADD 300950