Answer:
The 95% confidence interval is ( 27.126 , 34.674)
Explanation:
Given
The t critical value at 0.05 level = 2.023 for the df = 39
Confidence interval = 95%
Mean
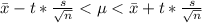
Substituting the given values we get -
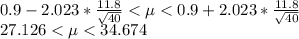
Hence, the 95% confidence interval is
( 27.126 , 34.674)