Answer:
The answer is below
Step-by-step explanation:
The z score is used to determine by how many standard deviations the raw score is above or below the mean. The z score is given by the formula:

For x > 780 hours:
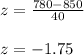
For x < 834 hours:
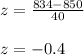
From the normal distribution table, P(780 < x < 834) = P(-1.75 < z < -0.4) = P(z < -0.4) - P(z < -1.75) = 0.3446 - 0.0401 = 0.3045 = 30.45%