Question

Peggy constructed the 95 percent confidence interval (4.8,5.2) to estimate the slope of a regression model for a set of bivariate data with 24 data values. Peggy claims that the width of the confidence interval will increase if a sample size of 30 is used, all other things remaining the same. Quincy claims that the width of the confidence interval will decrease if a sample size of 30 is used. Which statement is true about the claims made by Peggy and Quincy?

А. Peggy's claim is correct.
B. Quincy's claim is correct.
C. Both Peggy's claim and Quincy's claim are correct
D. Neither Peggy's claim nor Quincy's claim is correct.
E. There is not enough information to determine whether the claims are correct.

Answer 1

B. Quincy's claim is correct.

Explanation:

Margin of error of a confidence interval:

The margin of error of a confidence interval has the following format:

`M = z(s)/(√(n))`

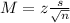
In which z is related to the confidence level, s is the standard error and n is the size of the sample.

From this interval, we have that the margin of error and the sample size are inversely proportional, that is, if we increase the sample size, the margin of error decreases, and so does the width of the confidence interval.

Peggy claims that the width of the confidence interval will increase if a sample size of 30 is used, all other things remaining the same.

Peggy is wrong, as the increase of the sample size results on the decrease of the margin of error, and a decrease of the width.

Quincy claims that the width of the confidence interval will decrease if a sample size of 30 is used.

Margin of error decreases, and so does the width of the interval, thus, Quincy's claim is correct, and the correct answer is given by option b.