Answer:
13
Explanation:
AB is bisected by perpendicular OC so AB is divided into intwo two equal halves.
if AB = 24
AC =
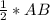
=
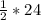
=12
no join OA and name its length as x
OA = X
OC = 5
AC = 12
when u join O and A it forms a triangle . SO to find OA lets find pythagoras theorem
OC^2 + AC^2 = OA^2
5^2 + 12^2 = OA^2
25 + 144 = OA^2
169 = OA^2
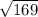 = OA
= OA
13 = OA
radius is the line joining the centre and any point on the circumference.So here since O is the centre and A is the points on the circumference and they are joined so the line can be named as radius of a circle.
Therefore radius of a circle is 13