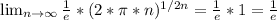Question

Please calculate this limit
please help me​

Answer 1

We want to find:

`\lim_(n \to \infty) \frac{\sqrt[n]{n!} }{n}`

Here we can use Stirling's approximation, which says that for large values of n, we get:

`n! = √(2*\pi*n) *((n)/(e) )^n`

Because here we are taking the limit when n tends to infinity, we can use this approximation.

Then we get.

`\lim_(n \to \infty) \frac{\sqrt[n]{n!} }{n} = \lim_(n \to \infty) \frac{\sqrt[n]{√(2*\pi*n) *((n)/(e) )^n} }{n} = \lim_(n \to \infty) (n)/(e*n) *\sqrt[2*n]{2*\pi*n}`

Now we can just simplify this, so we get:

`\lim_(n \to \infty) (1)/(e) *\sqrt[2*n]{2*\pi*n} \\`

And we can rewrite it as:

`\lim_(n \to \infty) (1)/(e) *(2*\pi*n)^(1/2n)`

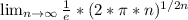
The important part here is the exponent, as n tends to infinite, the exponent tends to zero.

Thus:

`\lim_(n \to \infty) (1)/(e) *(2*\pi*n)^(1/2n) = (1)/(e)*1 = (1)/(e)`