Question

\left(a+b\right)^2 hihihihihiihihihihihih

Answer 1

Consider, we need to find the expanded form of the given expression.

Given:

The expression is:

`\left(a+b\right)^2`

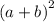
To find:

The expanded form of the given expression.

Solution:

We have,

`\left(a+b\right)^2`

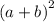
It can be written as:

`\left(a+b\right)^2=(a+b)(a+b)`

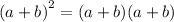
Using distributive property of multiplication over addition, we get

`\left(a+b\right)^2=a(a+b)+b(a+b)`

`\left(a+b\right)^2=a(a)+a(b)+b(a)+b(b)`

`\left(a+b\right)^2=a^2+ab+ab+b^2`

`\left(a+b\right)^2=a^2+2ab+b^2`

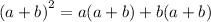
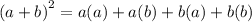
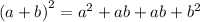
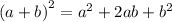
Therefore, the expanded form of the given expression is
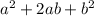`a^2+2ab+b^2`.