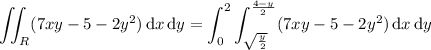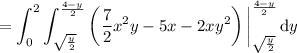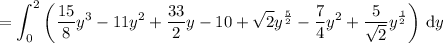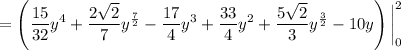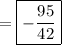Question

Compute ∬_R〖(7xy-5-2y^2)dxdy〗 where the domain of integration R is bounded by the lines y=0, y=4-2x and y=2x^2

Answer 1

Attached you'll find the region of interest, which is captured by the set of points

R = √(y/2) ≤ x ≤ (4 - y)/2 and 0 ≤ y ≤ 2

Written in this way, it's convenient to integrate with the order dx dy (that is, with respect to x first). In particular, we have

`\displaystyle\iint_R(7xy-5-2y^2)\,\mathrm dx\,\mathrm dy = \int_0^2 \int_(√(\frac y2))^{\frac{4-y}2} (7xy-5-2y^2)\,\mathrm dx\,\mathrm dy`

`\displaystyle = \int_0^2 \int_(√(\frac y2))^{\frac{4-y}2} \left(\frac72 x^2y-5x-2xy^2\right)\bigg|_(√(\frac y2))^{\frac{4-y}2}\,\mathrm dy`

`=\displaystyle\int_0^2\left(\frac{15}8y^3-11y^2+\frac{33}2y-10 +\sqrt2 y^(\frac52)-\frac74y^2+\frac5{\sqrt2}y^(\frac12)\right)\,\mathrm dy`

`=\displaystyle\left((15)/(32)y^4+\frac{2\sqrt2}7y^(\frac72)-\frac{17}4y^3+\frac{33}4y^2+\frac{5\sqrt2}3y^(\frac32)-10y\right)\bigg|_0^2`

`=\boxed{-(95)/(42)}`