Given:
The expressions are
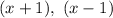 and
and
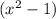 .
.
To find:
The least common multiple of given expressions.
Solution:
The expressions are
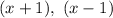 and
and
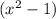 . The factor forms of these expressions are:
. The factor forms of these expressions are:
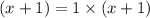

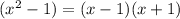
![[\because a^2-b^2=(a-b)(a+b)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/85p639al2fqbkfpvaacm253m69siuprplr.png)
The least common multiple is the product of all distinct factors with its highest degree. So,
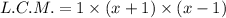
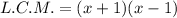
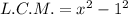
![[\because a^2-b^2=(a-b)(a+b)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/85p639al2fqbkfpvaacm253m69siuprplr.png)
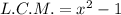
Therefore, the least common multiple of given expressions is
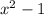 .
.