Question

The sides of a triangular plot are in the ratio 3 : 5 : 7 and its perimeter is 300 m. find its area​

Answer 1

Given :

• The sides of a triangular plot are in the ratio 3 : 5 : 7 .
• Its perimeter is 300 m.

⠀

To Find :

• Its area.

⠀

Solution :

• Let us assume the sides in metres be 3x, 5x and 7x .

⠀

Then, We know,

`\qquad \sf \dashrightarrow \: 3x + 5x + 7x = 300 \: \: \: \: \: \: \: Perimeter_((Triangle))`

`\qquad \sf \dashrightarrow \: 15x = 300`

`\qquad \sf \dashrightarrow \: x = (300)/(15)`

`\qquad \bf\dashrightarrow \: x = 20`

⠀

So, The sides of the triangle are :

`\qquad \sf \dashrightarrow \: 3 * 20 \: m = \bf60 \: m`

`\qquad \sf \dashrightarrow \: 5 * 20 \: m = \bf 100 \: m`

`\qquad \sf \dashrightarrow \: 7 * 20 \: m = \bf140 \: m`

⠀

Now, Using Heron's formula :

We have,

`\qquad \sf \dashrightarrow \: s = ( {60 + 100 + 140}) \: m = 300 \: m`

`\qquad \sf \dashrightarrow \: s = \frac {60 + 100 + 140}2 \: m = 150 \: m`

⠀

And the Area will be :

`\qquad \sf \dashrightarrow \: √(150(150 - 60)(150 - 100)(150 - 140)) \: {m}^(2)`

`\qquad \sf \dashrightarrow \: √(150 * 90 * 50 * 10) \: \: {m}^(2)`

`\qquad \sf \dashrightarrow \: 1500 √(3) \: {m}^(2)`

Answer 2

2598m²

Explanation:

Figure :

`\setlength{\unitlength}{1 cm}\begin{picture}(0,0)\thicklines\qbezier(1, 0)(1,0)(3,3)\qbezier(5,0)(5,0)(3,3)\qbezier(5,0)(1,0)(1,0)\put(2.85,3.2){$\bf A$}\put(0.5,-0.3){$\bf C$}\put(5.2,-0.3){$\bf B$}\put(5,1){$\bf 3x $}\put(2.5, - .5){$\bf 7x $}\put(.5,1){$\bf 5x $}\put(4.5,4){$\bf not \: to \: scale \: $}\end{picture}`

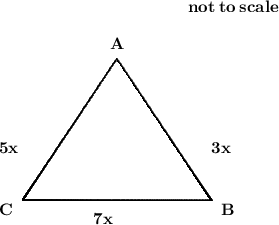
Here we are given that the ratio of sides of a triangular plot is 3:5:7 and its perimeter is 300m . We are interested in finding the area of the rectangle . Firstly , let us take the given ratio's HCF be x , then we may write the ratio as ,

`\longrightarrow 3x : 5x : 7x`

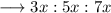
According to the question ,

`\longrightarrow 3x + 5x + 7x = 300m \\`

`\longrightarrow 15x = 300m\\`

`\longrightarrow x =(300m)/(15)\\`

`\longrightarrow x = 20m`

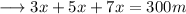
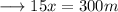
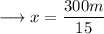
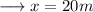
Therefore , the sides will be ,

`\longrightarrow 3x = 3(20m) = \red{60m}\\`

`\longrightarrow 5x =5(20m)= \red{100m}\\`

`\longrightarrow 7x =7(20m)=\red{140m}`

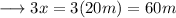
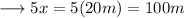
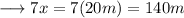
Now we may use Heron's Formula to find out the area of triangle as ,

Heron's Formula :-

• If three sides of a ∆ is a , b , c then the area is given by
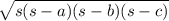  `√( s(s-a)(s-b)(s-c))` , where s is the semi perimeter .

Here ,

`\longrightarrow s =(300m)/(2)=150m`

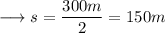
Therefore ,

`\longrightarrow Area =√( 150(150-60)(150-100)(150-140))m^2\\`

`\longrightarrow Area =√( 150 * 90 * 50 * 10)m^2\\`

`\longrightarrow Area = √( 50^2 * 30^2* 3)m^2\\`

`\longrightarrow Area = 50* 30 * 1.732 m^2\\`

`\longrightarrow\underline{\underline{ Area = 2598m^2}}`

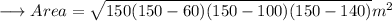
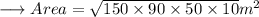
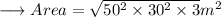
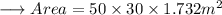
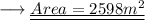
And we are done !