Answer:
a.

b.
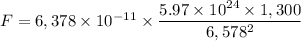
c.
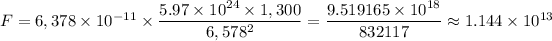
d. 1.144 × 10¹³ N
Step-by-step explanation:
The universal law of gravitation is presented as follows;

The given mass of the scientific satellite, m = 1,300 kg
The height of the orbit of the satellite, r = 200 km above the Earth's surface
The length of the radius of the Earth, R = 6378 km
The mass of the Earth = 5.97 × 10²⁴ kg
a. The formula for the universal law of gravitation is presented as follows;

Where;
M = The mass of the Earth = 5.97 × 10²⁴ kg
m = The mass of the satellite = 1,300 kg
r = The distance between the Earth and the satellite = R + r = 6,378 km + 200 km = 6,578 km
G = The Gravitational constant = 6.67430 × 10⁻¹¹ N·m²/kg²
b. Plugging in the values from the problem into the formula gives;
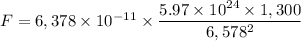
c. Solving gives;
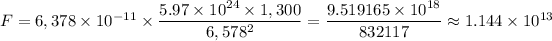
The force acting between the Earth and the satellite, F ≈ 1.144 × 10¹³ N
d. 1.144 × 10¹³ N