2 Answers

Ankor · Answer 1 · 2022-08-24T20:04:50+0000

Answer: Choice B

The range is
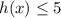
$h(x) \le 5$

==============================================================

Step-by-step explanation:

If we graph y = x+2, but only draw the line for x values smaller than 3, then we'll end up with the red line shown in the diagram below.

The blue line is the graph of y = -x+8, but it's only drawn when
$x \ge 3$

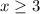
The two lines form an upside down V shape. This is an absolute value graph.

The highest point is at the vertex (3,5). The y coordinate is y = 5. This tells us that the largest h(x) can get is h(x) = 5.

Therefore, the range is
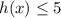
$h(x) \le 5$

This is the same as saying
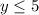$y\le 5$ since y and h(x) are both outputs of a function.

Andre Lombaard · Answer 2 · 2022-08-28T01:43:37+0000

9514 1404 393

Answer:

(b) h(x) ≤ 5

Step-by-step explanation:

The maximum vertical extent of the graph is h(x) = 5 at x = 3. The range is all values of h(x) less than or equal to that:

h(x) ≤ 5

Please log in or register to add a comment.