Question

I'm kinda lost here, what do I do when the quadrant is given? CanI have some of these solved at least with steps?

Answer 1

See Explaination

Explanation:

According To Question

• In Quadrant-1 (0* to 90*) ( All the Trignometry Functions are Positive )
• In Quadrant-2 (90* to 180*) (Only Sine & Cosecant are Positive)
• In Quadrant-3 (180* to 270*) (Only Tangent & Cotangent Are Positive)
• In Quadrant-4 (270* to 360*) ( Only Cosine & Secant Are Positive)

(Diagram, Please Find In Attachment)

Question 38 . Cos ∅ = 12/13 ∅ in Quadrant-4(Where only Cos & Sec are Positive all other Functions Are Negative in this Quadrant)

Now ∅ Represent a Right Angle Triangle with Base=12 Perpendicular=5 & Hypothenese=13

• other Five Trignometry Functions Are as Follow

Sin∅ = -5/13 , Cosec∅=-13/5 , Tan∅=-5/12 , Cot∅=-12/5 & Sec∅=13/12

Question 39 . SinX=-3/4 X Lies in Quadrant-3(Where only Tan & Cot are Positive all other Functions Are Negative in this Quadrant)

• Now For Other Trignometry Functions

Find By Using Basic Formulas

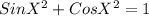`SinX^(2)+CosX^(2)=1` ↔ Put Value of Sin∅=-3/4

We get CosX= ±
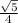`(√(5) )/(4)` (but X Lies in Quadrant-3 Where Cosine Is Negative , So Neglect CosX= +
`(√(5) )/(4)`)

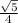So CosX= -
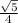`(√(5) )/(4)` ...... now you get the point . All Questions Will Solve like This .