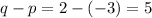Question

If p and q are the roots of 2x²+ 6x = 12 + 4x, and p < q, find q − p​

Answer 1

Explanation:

The given equation can be further simplified into

`2x^(2)+2x-12=0`

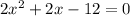
The roots of a quadratic equation is given by

`x = \frac{ - b \: \pm \: \sqrt{ {b}^(2) - 4ac} }{2a}`

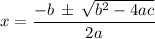
where a = 2, b = 2 and c = -12. Putting these into the roots equation, we get

`x = ( - 2 \: \pm \: √(4 \: - \: 4(2)( - 12)) )/(2(2)) = ( - 2 \: \pm \: 10)/(4)`

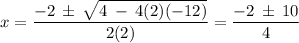
This gives us two possible roots:

x = 2, x = -3

Since the condition is that p < q, we see that p = -3 and q = 2. Therefore,

`q - p = 2 - ( - 3) = 5`