Answer:
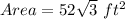
Explanation:
Area of trapezoid
 -----------( 1 )
-----------( 1 )
We will split the trapezoid into Triangle and rectangle. To find the height and full length of base.
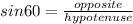
![[ opposite \ in \ the \ equation \ \ is \ the \ height \ of \ the \ trapezoid ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/4zayz11hv6jldaxxwlw5nx1tth4rlmsc6x.png)

Therefore, h = 4√3 ft
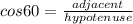
![adjacent \ in \ the\ equation \ is \ the\ base \ of \ the \ triangle ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/fx4qnxujnmu9pwhxuw91nl47kpdqj9tht1.png)

Therefore, a = 11 feet, b = 11 + 4 = 15 feet
Substitute the values in the Area equation :
