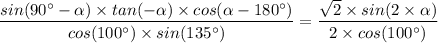Answer:
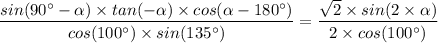
Step-by-step explanation:
The given expression is presented as follows;
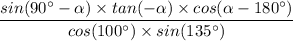
The sine, cosine, and tangent of the common angles are given as follows;
sin(A - B) = sin(A)·cos(B) - cos(A)·sin(B)
∴ sin(90° - α) = sin(90°)·cos(α) - cos(90°)·sin(α) = cos(α)
tan(-α) = -tan(α)
cos(A - B) = cos(A)·cos(B) + sin(A)·sin(B)
∴ cos(α - 180°) = cos(α)·cos(180°) + sin(α)·sin(180°) = -cos(α)
sin(135°) = sin(90° + 45°) = sin(90°)·cos(45°) + sin(45°)·cos(90°) = cos(45°) = √2/2
Therefore, we get;
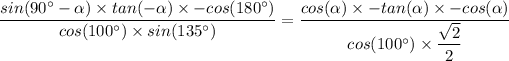
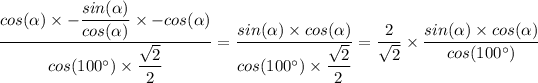
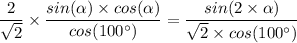
Therefore;