Question

A right triangle with the leg lengths of 7ft and 10ft. Using this information, find the length of the hypotenuse. Then round your answer to the nearest hundredth.

Answer 1

12.21

Step-by-step explanation:

Step-by-step explanation:

This is a right triangle, so the Pythagorean Theorem applies.

The Pythagorean Theorem states that the sum of the squared legs of a triangle is equal to the squared hypotenuse.

The legs of a triangle are the sides that form the right angle.

The hypotenuse of a triangle is the longest side.

Formula/solve:

`a^2+b^2=c^2`

`a,b-legs`

`c-hypotenuse`

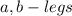
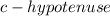
Here, I am solving for the hypotenuse.

`7^2+10^2=c^2`

`49+100=c^2`

`149=c^2`

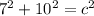
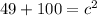
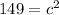
Conclude:

The last step is the cancel out c² by finding the square root of 149.

149 is not a perfect square, so I must round the square root to the nearest hundredth.

`12.2065556157` ≈
`12.21`

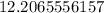I, therefore, believe the length of the hypotenuse is 12.21 feet.