Question

Solve each question (a, b, c) and show your work. Thank you <3

Answer 1

a) 112 ft.

b) 256 ft. and 3 seconds

c) 7 seconds

Explanation:

a) The model rocket is lauched from a platform. To find the height of the platform, we need to find h when t = 0, because the rocket starts from the platform when no time has elapsed:

`h=-16t^2+96t+112`

`h=-16*0+96+0+112\\\\h=112`

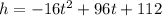
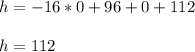
Therefore, the height of the platform is
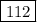`\fbox{112}` ft.

b) If you learned calculus before, we can find the maximum height easily. We take the derivative of h and set it equal to 0. Remember, the derivative of a function is simply the slope of it at an instantaneous point. At the maximum point of a function, it's slope equals to 0.

`h=-16t^2+96t+112\\h'=-32t+96+0\\h'=-32t+96`

Ok! Let's set the derivative of h to 0!

`0=-32t+96\\-96=-32t\\t=3`

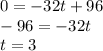
We now know how long it takes for the rocket to reach maximum point (t represents seconds), but we also need to find the maximum height. We can simply plug our t=3 into the function of h, because t=3 is the point where the rocket reaches maximum height:

`h(3)=-16(3)^2+96*3+112\\h(3)=-144+288+112\\h(3)=256`

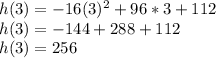
The maximum height of the rocket is
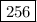`\fbox{256}` ft and the rocket takes
`\fbox{3}` seconds to reach the height.

c) The rocket reaches the ground when h equals 0. We can set up the equation to solve for it:

`h=-16t^2+96t+112\\0=-16t^2+96t+112\\0=-16(t+1)(t-7)\\0=(t+1)(t-7)\\t=-1, t=7`

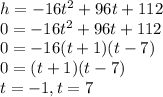
However, time can never be negative.

Therefore, it takes the rocket
`\fbox{7}` seconds to reach the ground.

I hope this helps! Let me know if you have any questions :)