Answer:
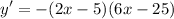
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Distributive Property
Algebra I
- Terms/Coefficients
- Factoring
Calculus
Derivatives
Derivative Notation
Derivative of a constant is 0
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Product Rule]:
![\displaystyle (d)/(dx) [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)](https://img.qammunity.org/2022/formulas/mathematics/college/c6fshhoq1mws6w0d0la17c7k2dcytwd8kg.png)
Derivative Rule [Chain Rule]:
![\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)](https://img.qammunity.org/2022/formulas/mathematics/high-school/vue68srn3fe6bds4idxorm97z7tgwelamw.png)
Explanation:
Step 1: Define
Identify
y = (2x - 5)²(5 - x)
Step 2: Differentiate
- Derivative Rule [Product Rule]:
 + (2x - 5)^2(d)/(dx)[(5 - x)]](https://img.qammunity.org/2022/formulas/mathematics/college/181orpn3a38trp9culx7pt4qglqbvrx2wp.png)
- Chain Rule [Basic Power Rule]:
![\displaystyle y' = [2(2x - 5)^(2 - 1) \cdot (d)/(dx)[2x]](5 - x) + (2x - 5)^2(d)/(dx)[(5 - x)]](https://img.qammunity.org/2022/formulas/mathematics/college/5v9oeue4tcehkqetv64tcr3324z660bcz1.png)
- Simplify:
![\displaystyle y' = [2(2x - 5) \cdot (d)/(dx)[2x]](5 - x) + (2x - 5)^2(d)/(dx)[(5 - x)]](https://img.qammunity.org/2022/formulas/mathematics/college/dcf1d7wu98dlxyqww1o4tewjbedb9vs7rj.png)
- Basic Power Rule:
 + (2x - 5)^2(1 \cdot -x^(1 - 1))]](https://img.qammunity.org/2022/formulas/mathematics/college/n1pffh0wukbw8ziqd3qkn3dnvitraxwo9j.png)
- Simplify:
 + (2x - 5)^2(-1)](https://img.qammunity.org/2022/formulas/mathematics/college/f8ifvfw8f9lm3vzbirm613p3a9rj7jmoc3.png)
- Multiply:
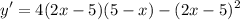
- Factor:
![\displaystyle y' = (2x - 5)[4(5 - x) - (2x - 5)]](https://img.qammunity.org/2022/formulas/mathematics/college/ggbletm2byk1gzkhdpg1o29w71wss5yg8i.png)
- [Distributive Property] Distribute 4:
![\displaystyle y' = (2x - 5)[20 - 4x - (2x - 5)]](https://img.qammunity.org/2022/formulas/mathematics/college/ditrd2tuye5e04qzbxt0cz5izizg8c4mdf.png)
- [Distributive Property] Distribute negative:
![\displaystyle y' = (2x - 5)[20 - 4x - 2x + 5]](https://img.qammunity.org/2022/formulas/mathematics/college/6e8zy16zpmm31hf6brnhniafo3jqge4y4u.png)
- [Subtraction] Combine like terms (x):
![\displaystyle y' = (2x - 5)[20 - 6x + 5]](https://img.qammunity.org/2022/formulas/mathematics/college/xyej232v29y5o260yhn5l0tg7c3j2mdxyk.png)
- [Addition] Combine like terms:
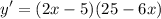
- Factor:
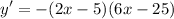
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Derivatives
Book: College Calculus 10e