Question

Tori is cutting fabric squares to make a quilt. Her squares on average are 5 in. on each side with a standard deviation of 0.1 in. If her cuts are normally distributed, what percentage of her squares would be between 4.9 and 5.1 in?

Answer 1

`\approx 68\%`

Explanation:

For normal distributions only, all data falls within approximately 68% of one standard deviation, 95% of two standard deviations, and close to 100% of three standard deviations. The standard deviation is far too small to represent two or three standard deviations, hence
`\implies \boxed{68\%}`.

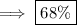*Important: This problem would be unsolvable if the question did not say her cuts were normally distributed, because the information above is only applicable to normal distributions.

Answer 2

• 68.26%

Explanation:

Given:

• Mean μ = 5 in
• Standard deviation σ = 0.1 in

The squares between 4.9 and 5.1 represent:

• x = 5 ± 0.1

Relevant z- scores are:

• z = (x - μ)/σ
• z = (5.1 - 5)/0.1 = 1
• z = (4.9 - 5)/0.1 = -1

From the z-score table we get:

• z = 1 ⇒ 84.13% mark
• z = -1 ⇒ 15.87% mark

The data between these points is:

• 84.13% - 15.87% = 68.26%