Question

Please help me!!

what is an equation in standard form of an ellipse centered at the origin with vertex (-4,0) and co-vertex (0,5)???

Answer 1

`(x^2)/(16)+(y^2)/(25)=1`

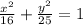
Explanation:

The equation of an ellipse with a center at
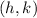`(h, k)` and vertices at
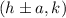`(h\pm a, k)` and
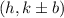`(h, k\pm b)` is given by
`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`.

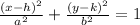Since two vertices are located at (-4, 0) and (0, 5), the other vertices must be located at (4, 0) and (0, -5).

What we know:

• Center of (0, 0)
• From
  `(h\pm a, k)`,
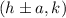  `a` must be 4
• From
  `(h, k\pm b)`,
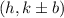  `b` must be 5

Thus, we have:

`((x-0)^2)/(4^2)+((y-0)^2)/(5^2)=1\implies \boxed{(x^2)/(16)+(y^2)/(25)=1}`