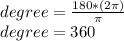Question

Does anyone know how to solve this?

Answer 1

x = 45°

Explanation:

Given arc length = 2π cm

Radius, r = 8 cm

`Arc \ Length = 2 \pi r ((x)/(360))`

`2 \pi = 2 \pi * 8 ( x)/(360)\\\\(2 \pi)/(16 \pi) = (x )/( 360)\\\\(1)/(8) = (x)/(360)\\\\(360)/(8) = x\\\\x = 45^\circ`

Answer 2

`x=360`

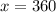
Explanation:

The inscribed angles theorem states that when given a circle, with an angle that has its vertex at the center of the circle, the measure of the angle is congruent to the measure of the arc surrounding it. One can apply this knowledge here by stating the following,

`m<MON = MN\\`

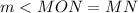
Substitute,

`x=2\pi`

However, this answer is in radians, it is the literal measurement. One must convert into degrees so that the answer fits the format of the question. The conversion rate to switch between radians and degrees is the following,

`degree=(\pi)/(180)radians`

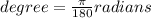
Substitute,

`degree=(180)/(\pi)(x)\\\\degree=(180)/(\pi)(2\pi)\\`

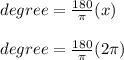
Simplify,

`degree=(180*(2\pi))/(\pi)\\degree=360`