Question

Helpppppppppoppppppppp

Answer 1

Explanation:

Using
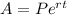`A=Pe^{rt` as instructed, our equation looks like this:

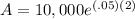`A=10,000e^((.05)(2))` which simplifies a bit to

`A=10,000e^{.1` which simplifies a bit more to

A = 10,000(1.10517) so

A = 11,051.71 Easy. Now onto the second part: solving for the number of years it takes for the investment to double. Setting A equal to 20,000 since 20,000 is 10,000 doubled:

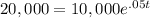`20,000=10,000e^{.05t` Begin by dividing both sides by 10,000 to get

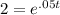`2=e^{.05t` and take the natural log of both sides to get that exponent down out front, keeping in mind that the natural log will "undo" the e, leaving us with:

ln(2) = .05t and

t = 14 years (that's 13.8 rounded up to the nearest year)

Answer 2

A)

Replace the letters in the given equation with the corresponding values given in the problem:

A = 10,000 x 2.718^(0.05 x 2)

A = 11,051.59 , rounded to nearest dollar = $11,052

B)20,000 = 10000 x 2.718^(0.05 x t)

Divide both sides by 10,000:

2 = 2.718^(0.05 x t)

Apply exponent rules:

0.05tln(2.718) = 2

Solve for t:

t = ln(2) / 0.05ln(2.718)

t = 13.86 years, rounded to nearest year = 14 years.