Question

Find the equation of a line perpendicular to x+5y=−2 that contains the point (3,0).

Answer 1

Perpendicular Definition:

`\large \boxed{m_1m_2 = - 1}`

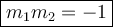
Slopes of two different equations multiply each others and must equal to -1. We can also say that the perpendicular occurs only if both equations are negative reciprocal to each others. For example, we are given the equation of y = 2x. The perpendicular to y = 2x would be y = (-1/2)x. See how both are reciprocal to each others.

From the equation below:

`\large{x + 5y = - 2}`

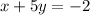
Since the equation is in the form of Ax+By = C. It is better to use the another slope formula which is:

`\large \boxed{m = - (A)/(B) }`

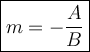
From the equation above, use the slope formula to find the slope.

`\large{m = - (1)/(5) }`

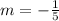
Therefore the equation has a slope of -1/5. Next to find the perpendicular equation to the original equation. Since our slope is -1/5 - that means the negative reciprocal of -1/5 is 5. Therefore the slope of perpendicular line is 5.

Next we will be using the point-slope form below:

`\large \boxed{y - y_1 = m(x - x_1)}`

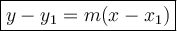
Given the y1 and x1 or (x1,y1) are the points. Our perpendicular slope is 5 which passes through the point (3,0). Substitute both slope and the point in.

`\large{y - 0 = 5(x - 3)}`

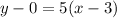
Simplify in the slope-intercept form as we get:

`\large{y = 5x - 15}`

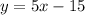
Answer

• y = 5x-15 is perpendicular to x+5y = -2

Hope this helps and let me know if you have any doubts!