Question

Find the equation of a line that contains the points (0,0) and (6,−7). Write the equation in slope-intercept form, using fractions when required.

Answer 1

Use the slope formula below:

`\large \boxed{m = (y_2 - y_1)/(x_2 - x_1) }`

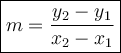
To form an equation of a line - we need to find a slope and the y-intercept from y = mx+b. We are given two points which we can substitute in the formula.

`\large{m = (0 - ( - 7))/(0 - 6) } \\ \large{m = (0 + 7)/( - 6) \longrightarrow (7)/( - 6) } \\ \large \boxed{m = - (7)/(6) }`

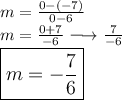
We have finally got the slope. Next is to find the y-intercept. First we rewrite the equation of y = mx+b by substituting the slope.

`\large \boxed{y = mx + b}`

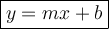
The equation above is the slope-intercept form. Substitute m = -7/6 in the equation.

`\large{y = - (7)/(6) x + b}`

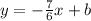
Since the graph passes through (0,0) which is an origin point. In y = mx+b if the graph passes through origin point, that means the b-value is 0. Therefore:

`\large \boxed{y = - (7)/(6) + 0 \longrightarrow y = - (7)/(6) x}`

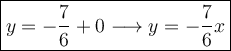
Answer

• y = -7x/6

Hope this helps and let me know if you have any doubts! Good luck on your assignment!