Question

2x-5y=-3
5x+2y=6
Is this a perpendicular lines ?

Answer 1

Perpendiculat Line is when both slopes of equation multiplying each others and equal to -1.

`\large \boxed{m_1m_2 = - 1}`

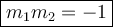
For an easier way to understand, a perpendicular line has a negative reciprocal slope. For example if we are given the equation of y = 2x then the equation that is perpendicular to y = 2x would be y = (-1/2)x.

From both equations. We can either arrange in slope-intercepy form or use the slope formula which is m = -A/B when the equation is in Ax+By+C = 0 or Ax+By = C.

`\large{ \begin{cases} 2x - 5y = - 3 \\ 5x + 2y = 6 \end{cases}}`

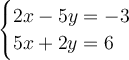
To find if these two lines are perpendicular to each others. Use the slope formula of -A/B.

`\large{ \begin{cases} m_1 = - (2)/( - 5) \\ m_2 = - (5)/(2) \end{cases}} \\ \large{ \begin{cases} m_1 = (2)/( 5) \\ m_2 = - (5)/(2) \end{cases}}`

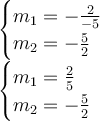
Now recall that it is perpendicular when one of them is negative reciprocal of one another (-5/2 is negative reciprocal of -(-2/5) = 2/5 and 2/5 is negative reciprocal of -5/2).

Or in definition of perpendicular lines, both slopes multiply and must equal to -1.

`\large{( (2)/(5) )( - (5)/(2) ) = - 1} \\ \large{ - 1 = - 1}`

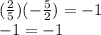
Thus the equation is true which makes both lines perpendicular to each others.

Answer

• Both lines are perpendicular to each others.

Let me know if you have any doubts!