Question

Answer this question ( Steps required ) Please help​

Answer 1

9514 1404 393

Answer:

(2ac+1)/(abc+2c+1)

Explanation:

It helps to understand the factoring of the numbers involved.

63 = 3²·7

140 = 2²·5·7

The "change of base" formula is also useful.

`\log_b{a}=\frac{\log{a}}{\log{b}}`

__

Using this, we can write ...

a = log(3)/log(2) ⇒ log(3) = a·log(2)

b = log(5)/log(3) ⇒ log(5) = b·log(3) = ab·log(2)

c = log(2)/log(7) ⇒ log(2) = c·log(7)

This lets us write everything in terms of log(7):

log(2) = c·log(7)

log(3) = ac·log(7)

log(5) = abc·log(7)

__

The desired logarithm is ...

`\log_(140){}63=\frac{\log{63}}{\log{140}}=\frac{2\log{(3)}+\log{(7)}}{2\log{(2)}+\log{(5)}+\log{(7)}}\\\\=\frac{2ac\cdot\log{(7)}+\log{(7)}}{2c\cdot\log{(7)}+abc\cdot\log{(7)}+\log{(7)}}\\\\\boxed{log_140(63)=(2ac+1)/(abc+2c+1)}`

_____

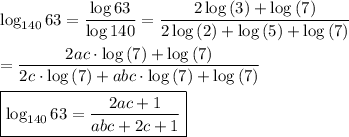
The attachment is a numerical check of this result.