Answer:
Approximately
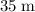 .
.
Explanation:
In a right triangle, the tangent of an angle is the ratio between the length of the side opposite to this angle and the length of the side adjacent to this angle:
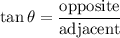 .
.
Let
 denote the height of this kite in meters.
denote the height of this kite in meters.
Refer to the diagram attached. Let
 denote the point right below the kite in the same vertical plane as
denote the point right below the kite in the same vertical plane as
 and
and
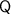 . Denote the kite as
. Denote the kite as
 .
.
The kite
 , observer
, observer
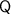 , and point
, and point
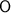 are the three vertices of right triangle
are the three vertices of right triangle
 , where
, where
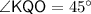 .
.
In this right triangle,
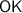 is the side opposite to
is the side opposite to
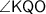 , whereas
, whereas
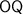 is the side adjacent to
is the side adjacent to
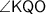 .
.
Therefore:
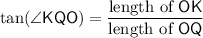 .
.
- The length of
 is the same as the height of this kite,
is the same as the height of this kite,
 meters.
meters. - The length of
 denotes the horizontal distance between the kite and observer
denotes the horizontal distance between the kite and observer
 .
.
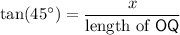 .
.
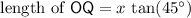 .
.
Similarly, in right triangle
 ,
,
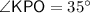 . In this right triangle,
. In this right triangle,
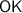 is the side opposite to
is the side opposite to
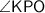 , whereas
, whereas
 is the side adjacent to
is the side adjacent to
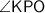 .
.
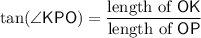 .
.
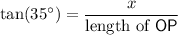 .
.
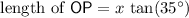
The question states that observer
 and observer
and observer
 are on the same side of the kite. Hence, the horizontal distance between
are on the same side of the kite. Hence, the horizontal distance between
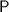 and
and
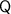 would be the same as the difference between:
would be the same as the difference between:
- the horizontal distance between
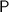 and the kite (same as the length of segment
and the kite (same as the length of segment
 ,) and
,) and - the horizontal distance between
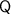 and the kite (same as the length of segment
and the kite (same as the length of segment
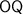 .)
.)
In other words:
 .
.
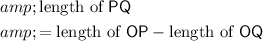 .
.
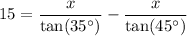 .
.
Solve for
 :
:
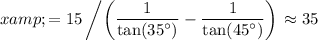 .
.