Given:
In the given figure,
 , WS = 5, WR = 4x+3, RT=7x+3 and VT=8.
, WS = 5, WR = 4x+3, RT=7x+3 and VT=8.
To find:
The measure of WR and RT.
Solution:
In triangles WRS and TRV,
 (Given)
(Given)
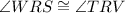 (Vertically opposite angles)
(Vertically opposite angles)
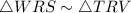 (AA property of similarity)
(AA property of similarity)
We know that the corresponding sides of similar triangles are proportional. So,
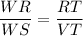


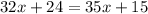
Isolate the variable x.
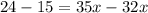
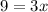
Divide both sides by 3.
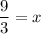
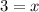
Now,
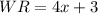
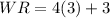

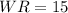
And,
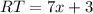

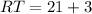
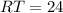
Therefore, the measure of WR is 15 units and the measure of RT is 24 units.