Answer: You have the correct answer. It's choice B
Domain =
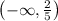
Nice work.
=========================================================
Step-by-step explanation:
The domain of g(x) is found by setting 2-5x greater than or equal to 0 and solving for x. We're doing this to ensure that 2-5x is not negative.

So we can plug in any number smaller than 2/5, or we can plug in 2/5 itself, into the g(x) function to get some output.
However, notice that if x = 2/5, then g(x) = 0. This then would feed into the f(x) function and lead to a division by zero error. Therefore, x = 2/5 must be kicked out of the domain of (f o g)(x). We keep everything else that we found earlier.
In short, the domain as an inequality is
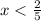 , which is the same as saying
, which is the same as saying
 and that converts to the interval notation
and that converts to the interval notation
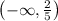
We don't use a square bracket because we don't want to include the endpoint 2/5.