Question

What is the value of A when we rewrite 1.44^1.2x as A^x​

Answer 1

a = 0.64

Explanation:

hope that helped

Answer 2

The correct expression for A in the given problem is option C:
`A=1.44^((-1.2))`

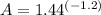
Let's rewrite
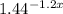`1.44^(-1.2 x)` as
`A^x` and then compare it to the given options:

`1.44^(-1.2 x)=A^x`

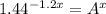
Now, let's express 1.44 in terms of A:

`A=1.44^((-1.2))`

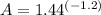
Now, let's substitute this value of A back into the original equation:

`1.44^(-1.2 x)=\left(1.44^((-1.2))\right)^x`

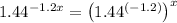
Now, compare this expression with the provided options:

`A=1.44^((-1.2))`

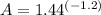
Certainly! Let's rewriteB.
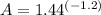`A=1.44^((-1.2))` as Ax:

A=1.44^{(-1.2)} - AX

Now, let's take the natural logarithm (ln) of both sides to simplify the exponent

In (¹.⁴⁴¹.²ˣ) - In (Ax)

Using the property In ⁽ᵃᵇ⁾ -b In(a) we can bring down the exponent:

1.2xln(1.44)=xln(A)

Now, solve for A: n(A)= 1.2ln(1.44/1)

ln(A)=0.1392

Now, exponentiate both sides to solve for A:

A=e 0.1392

So, A is approximately equal to:

A≈1.1496

Therefore, when you rewrite ¹.⁴⁴¹.²ˣ as ᴬ, the value of A is approximately 1.1496.