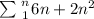Question

Who do I solve this I have only 10 minuted​

Answer 1

`\sum {{n} \atop {1}} \right 6n+2n^2`

Explanation:

Given the series 8 + 12 + 16 + 20+ ...

Sum of nth term Sn = n/2[2a+(n-1)d]

a is the first term = 8

d is the common difference = 12 - 8 = 16 - 12 = 4

Substitute

Sn = n/2[2(8)+(n-1)(4)]

Sn = n/2[16+4n-4]

Sn = n/2[12+4n]

Sn 2n/2[6+2n]

Sn = n(6+2n)

Sn = 6n + 2n²

Hence the sigma representation is expressed as;

`\sum {{n} \atop {1}} \right 6n+2n^2`