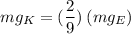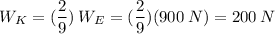(C) 200 N
Step-by-step explanation:
The acceleration due to gravity on earth
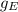 is given by
is given by
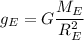
where
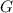 = universal gravitational constant
= universal gravitational constant
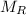 = mass of the earth
= mass of the earth
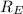 = radius of the earth
= radius of the earth
Planet Krypton has twice the mass of earth and 3 times the radius so its acceleration due to gravity
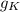 is
is
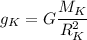
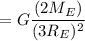
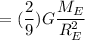
or
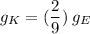
If we multiply both sides by Superman's mass, we get his weights on both planets: