Question

The volume of a cylinder is 1087 cm and its height is 12 cm.

Answer 1

Explanation:

Appropriate QuestioN :

• The volume of a cylinder is 108π cm³ and its height is 12 cm. What is the length of the cylinder's radius?

Need to FinD :

• We have to find the length of the cylinder's radius.

`\red{\frak{Given}} \begin{cases} & \sf{Volume\ of\ the\ cylinder\ =\ {\pmb{\sf{108{\pi}\ cm^3.}}}} \\ & \sf{Height\ of\ the\ cylinder\ =\ {\pmb{\sf{12\ cm.}}}} \end{cases}`

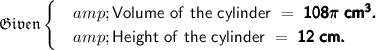
We know that,

• The volume of a cylinder is the density of the cylinder which shows the amount of material contained in the cylinder.
• The volume of the cylinder is given by, πr²h.

Where,

• r is for radius.
• h is for height.

`\rule{200}{3}`

• Now, let's calculate the length of the cylinder's radius.

`\sf \dashrightarrow {Volume\ of\ cylinder\ =\ {\pi}r^2h} \\ \\ \\ \sf \dashrightarrow {108{\pi}\ =\ {\pi}r^2h} \\ \\ \\ \sf \dashrightarrow {108{\cancel \pi}\ =\ {\cancel \pi}r^2 * 12} \\ \\ \\ \sf \dashrightarrow {108\ =\ r^2 * 12} \\ \\ \\ \sf \dashrightarrow {\frac{\cancel{108}}{\cancel{12}}\ =\ r^2} \\ \\ \\ \sf \dashrightarrow {r^2\ =\ 9} \\ \\ \\ \sf \dashrightarrow {r\ =\ √(9)} \\ \\ \\ \dashrightarrow {\underbrace{\boxed{\pink{\frak{r\ =\ 3\ cm.}}}}_{\sf \blue{\tiny{Radius\ of\ cylinder}}}}`

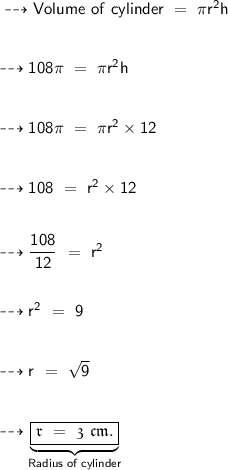
∴ Hence, the length of the cylinder's radius is 3 cm.