Question

Determine the value of k

Answer 1

k=6

Explanation:

For a piecewise function to be continuous, the left-side and right-side limits must be equal to each other. Therefore, the left-side limit of f(x) is 8 because the derivative of 2x^2 is 4x, and then directly substituting x=2 gives us 4(2)=8. Therefore, the right-side limit must also equal 8. Therefore, k must be 6 because 2+6=8.

Answer 2

`\displaystyle k = 6`

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

• Multiplication Property of Equality
• Division Property of Equality
• Addition Property of Equality
• Subtraction Property of Equality

Algebra I

• Functions
• Function Notation

Algebra II

• Piecewise Functions

Calculus

• Limits
• Continuity

Explanation:

Step 1: Define

Identify

Continuous at x = 2

`\displaystyle f(x) = \left \{ {{2x^2 \ if \ x < 2} \atop {x + k \ if \ x \geq 2}} \right.`

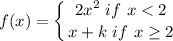
Step 2: Solve for k

1. Definition of Continuity:
   `\displaystyle \lim_(x \to 2^+) 2x^2 = \lim_(x \to 2^-) x + k`
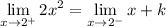
2. Evaluate limits:
   `\displaystyle 2(2)^2 = 2 + k`
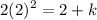
3. Evaluate exponents:
   `\displaystyle 2(4) = 2 + k`
4. Multiply:
   `\displaystyle 8 = 2 + k`
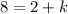
5. [Subtraction Property of Equality] Subtract 2 on both sides:
   `\displaystyle 6 = k`
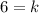
6. Rewrite:
   `\displaystyle k = 6`

Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Limits - Continuity

Book: College Calculus 10e