Question

Questions on file. Pls halp

Answer 1

1)

V = l * w * h

7/4 * 3/2 * 1/2 = 21/16 cm^3

2)

A = a+b ÷ 2 * h

6 + 4 = 10 ÷ 2 = 5

5 * 3 = 15 ft^2

Answer 2

`\large{ \tt{❋ \: EXPLANATION}} :`

• The formula to find out the volume of a rectangular prism is V = l × b × h where V is the volume , l = length , b = breadth & h = height.

• We're provided the figure of trapezium in the second attachment. The formula to fInd out the area of trapezium is A =
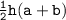  `\tt{ (1)/(2) h(a + b)}` where a and b are the opposite parallel sides and h be the height of a trapezium.

`\large{ \tt{❃ \: SOLUTION}} :`

• In the first picture , we're provided - Length ( l ) =
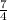  `(7)/(4)` cm , breadth ( b ) =
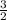  `(3)/(2)` cm and height ( h ) =
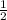  `(1)/(2)` cm. Now, plug these known values and them find out the volume of given rectangular prism.

`\large{ \tt{❁ \: VOLUME \: OF \: RECTANGULAR \: PRISM \: ( \: V \: ) = l * b * h}}`

`\large{ {⟶ \: (7)/(4) * (3)/(2) * (1)/(2) }}`

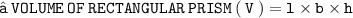
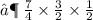
• To multiply one fraction by another , multiply the numerators for the numerator and multiply the denominator for its denominator and reduce the fraction obtained after multiplication into lowest term if possible.

`\large{ ⟶ (7 * 3 * 1)/(4 * 2 * 2) }`

`\large{⟶ (21)/(16) \tt{ {cm}^(3) }}`

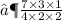
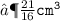
• Hence , the volume is
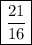  `\boxed{ (21)/(16) }` cubic centimetres.

--------------------------------

• In the second attachment , we're provided - 6ft and 7 ft are the opposite parallel sides and 3 ft is the height of the given trapezium.

`\large{ \tt{✺ \: AREA \: OF \: A \: TRAPEZIUM = (1)/(2) h(a + b)}}`

`\large{ ⟶ (1)/(2) * 3(6 + 7)}`

`\large{⟶ \: (1)/(2) * 3 * 13 }`

`\large{⟶ (39)/(2) \tt{cm}^(2) }`

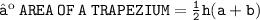
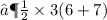
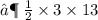
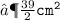
• Hence , The area of trapezium is
  `\boxed{ (39)/(2) \tt{cm}^(2) }`

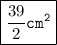
And we're done ! ♪

`\large{ \# \: \mathfrak{StayInAndExplore \:☂ }}`

▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁