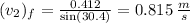Question

A pool ball moving 1.33 m/s strikes an identical ball at rest. Afterward, the first ball moves 0.750 m/s at a 33.30 angle. What is the velocity of the other ball?

Answer 1

Step-by-step explanation:

We need to apply the conservation law of linear momentum to two dimensions:

Let
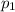`p_(1)` = momentum of the 1st ball

`p_(2)` = momentum of the 2nd ball

In the x-axis, the conservation law can be written as

`(p_(1) \cos \theta_(1))_(i) + (p_(2) \cos \theta_(2))_(i) = (p_(1) \cos \theta_(1))_(f) + (p_(2) \cos \theta_(2))_(f)`

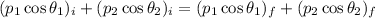
or

`(m_(1)v_(1))_(i)= (m_(1)v_(1)\cos \theta_(1))_(f) + (m_(2)v_(2)\cos \theta_(2))_(f)`

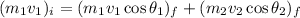
Since we are dealing with identical balls, all the m terms cancel out so we are left with

`(v_(1))_(i) = (v_(1))_(f)\cos \theta_(1) + (v_(2))_(f)\cos \theta_(2)`

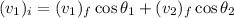
Putting in the numbers, we get

`1.33 = (0.750) \cos(33.30) + (v_(2))_(f) \cos \theta_(2)`

`= > (v_(2))_(f) \cos \theta_(2) = 0.703`

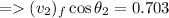
In the y-axis, there is no initial y-component of the momentum before the collision so we can write

`0 = (v_(1)\sin \theta_(1))_(f) + (v_(2)\sin \theta_(2))_(f)`

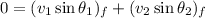
or

`= > (v_(2))_(f) \sin \theta_(2) = (0.750) \sin(33.30) = 0.412`

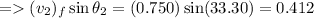
Taking the ratio of the sine equation to the cosine equation, we get

`( \sin \theta _(2))/( \cos \theta_(2) ) = \tan \theta_(2) = (0.412)/(0.703) = 0.586`

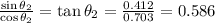
or

`\theta_(2) = { \tan}^( - 1) (0.586) = 30.4`

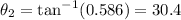
Solving now for
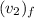`(v_(2))_(f)`,

`(v_(2))_(f) = (0.412)/( \sin(30.4) ) = 0.815 \: (m)/(s)`