Question

A 2890-lb car is traveling with a speed of 58 mi/hr as it approaches point A. Beginning at A, it decelerates uniformly to a speed of 18 mi/hr as it passes point C of the horizontal and unbanked ramp. Determine the total horizontal force F exerted by the road on the car just after it passes point B.

Answer 1

4592.57 lb

Step-by-step explanation:

The missing diagram for this question is attached in the image below.

Given that:

the weight of the car = 2890 lb

At point A, the speed of the car
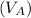`(V_A)` = 58 mi/hr

At point C, the speed of the car
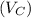`(V_C)` = 18 mi/hr

To ft/s:

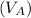`(V_A)` = 58 mi/hr × 5280 ft/1 mi × 1 hr/3600 s

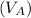`(V_A)` = 85.07 ft/s

`(V_C)` = 18 mi/hr × 5280 ft/1 mi × 1 hr/3600 s

`(V_C)` = 26.4 ft/s

Between A to C, the total distance is;

`S_(AC) = S_(AB)} + S_(BC) \\ \\ S_(AC) = 331 + (\pi r)/(2) \\ \\ S_(AC)= 331 + (\pi * 207)/(2) \\ \\ S_(AC) = 656.154 \ ft`

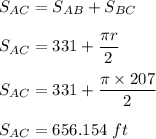
Now, we need to determine the deceleration of the car using the formula:

`V_C^2 = V_A^2 + 2 aS_(AC)`

`26.4^2 = 85.07^2 + 2 a (654.154)`

`696.96 = 7236.9049+ 2 a (654.154)`

`696.96-7236.9049 = 2 a (654.154)`

`-6539.9449 = 2 a (654.154)`

`a= \frac{-6539.9449} {2(654.154)}`

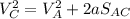
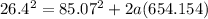
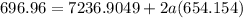
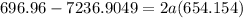
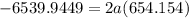
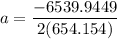
a = -4.99 ft/s²

The velocity of the car as it passes via B

`v_B^2 = v_A^2 + 2aS_(AB)`

`v_B^2 = 85.07^2 + 2(-4.99 * 331)`

`v_B =√( 85.07^2 + 2(-4.99 * 331))`

`v_B =√( 85.07^2 +3303.38)`

`v_B =√( 10540.2849)`

`v_B =102.67 \ ft/s`

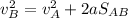
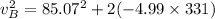
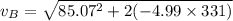
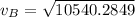
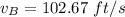
Along B, the car's acceleration is:

`a_B = \sqrt{a^2 + ((v_B^2)/(r))^2}`

`a_B = \sqrt{(-4.99)^2 + (102.67^2)/(207)^2 }`

`a_B = 51.17 \ ft/s^2`

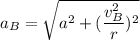
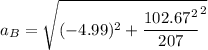
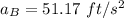
Finally, the total horizontal force F exerted = m
`a_B`

`= ((2890)/(32.2)) * 51.17`

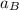
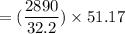
= 4592.57 lb