Question

The variance in a production process is an important measure of the quality of the process. A large variance often signals an opportunity for improvement in the process by finding ways to reduce the process variance. Conduct a statistical test to determine whether there is a significant difference between the variances in the bag weights for the two machines. Use a level of significance. What is your conclusion? Which machine, if either, provides the greater opportunity for quality improvements? Click on the datafile logo to reference the data. (to 4 decimals) (to 4 decimals) (to 2 decimals) - Select your answer -

Answer 1

There is a sufficient evidence to support the that machine 1 has the greater variance.

Explanation:

The question with the complete details can be found online.

Start by stating the hypotheses.

The null hypothesis states that the variance of machine 1 is less than or equal to machine 2

So, we have:

`H_o: \sigma_1 ^2 \le \sigma_2 ^2`

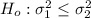
The alternate hypothesis will then be:

`H_a: \sigma_1 ^2 > \sigma_2 ^2`

So, we have:

`n_1 = 25`
`n_1 = 22`

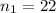
Calculate the mean of Machine 1 and 2

The mean is:

`\bar x =(\sum x)/(n)`

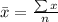
For machine 1, we have:

`\bar x_1 =(2.95+3.45+3.5+.....+3.12)/(25)`

`\bar x_1 =(83.21)/(25)`

`\bar x_1 =3.3284`

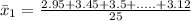
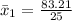
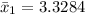
For machine 2, we have:

`\bar x_2 = (3.22 + 3.3 + 3.34 + ..... +3.33)/(22)`

`\bar x_2 = (72.12)/(22)`

`\bar x_2 = 3.2782`

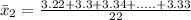
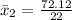
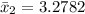
Calculate the standard deviation of both machines

The standard deviation is:

`\sigma = \sqrt{(\sum(x - \bar x)^2)/(n-1)}`

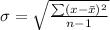
For machine 1, we have:

`\sigma_1 = \sqrt{((2.95 - 3.3284)^2+(3.45 - 3.3284)^2+(3.5 - 3.3284)^2+.....+(3.12 - 3.3284)^2)/(25-1)}`

`\sigma_1 = \sqrt{((2.95 - 3.3284)^2+(3.45 - 3.3284)^2+(3.5 - 3.3284)^2+.....+(3.12 - 3.3284)^2)/(24)}`

`\sigma_1 = 0.2211`

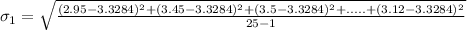
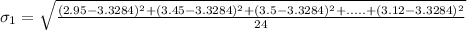
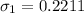
For machine 2, we have:

`\sigma_2 = \sqrt{((3.22 - 3.2782)^2+(3.3 - 3.2782)^2+(3.44 - 3.2782)^2+.....+(3.33 - 3.2782)^2)/(22-1)}`

`\sigma_2 = \sqrt{((3.22 - 3.2782)^2+(3.3 - 3.2782)^2+(3.44 - 3.2782)^2+.....+(3.33 - 3.2782)^2)/(21)}`

`\sigma_2 = 0.0768`

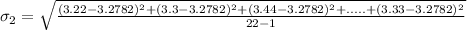
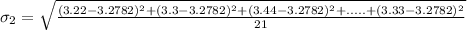
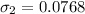
Calculate the degrees of freedom

`df=n-1`

For machine 1;

`df_1=25-1=24`

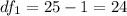
For machine 2

`df_2=22-1=21`

Calculate the test statistic (t)

`t = (Var_1)/(Var_2)`

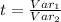
Rewrite in terms of standard deviation

`t = (\sigma_1^2)/(\sigma_2^2)`

`t = (0.2211^2)/(0.0768^2)`

`t = (0.04888521)/(0.00589824)`

`t = 8.2881`

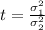
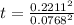
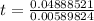
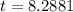
Lastly, calculate the p value.

This is the value of P(t > 8.2881) between the degrees of freedom i.e. 21 and 24

From the f distribution table

`P(t > 8.2881) < 0.01`

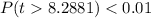
Hence, we reject the null hypothesis