Answer:
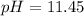
Step-by-step explanation:
Hello there!
In this case, since the chemical equation representing the neutralization of the weak base quinine can be written as follows:
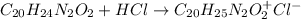
Whereas we have 0.100 moles of the base and those of acid as shown below
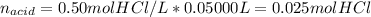
Which means that the remaining moles of quinine are:
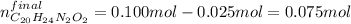
And the resulting concentration:
![[C_(20)H_(24)N_2O_2]=(0.075mol)/((0.025+0.050)L) =1.00M](https://img.qammunity.org/2022/formulas/chemistry/college/oukyvlixdoswysfyartavkyna6023b31qp.png)
Now, the calculation of the pH requires the pKb of quinine (5.1) as its ionization in water produces OH- ions:
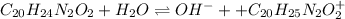
And the equilibrium expression is:
![Kb=([C_(20)H_(24)N_2O_2][C_(20)H_(25)N_2O_2 ^+])/([C_(20)H_(24)N_2O_2]) \\\\10^(-5.1)=(x^2)/(1.00M)\\\\ 7.94x10^(-6)=(x^2)/(1.00M)](https://img.qammunity.org/2022/formulas/chemistry/college/87y6xagg2z9hmh70gij9chfiudzysuwm1x.png)
Which is solved for x as follows:
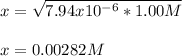
Which means the pOH is:
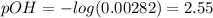
And the pH:
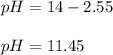
Regards!