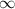Question

Q2/Deceleration of a particle is based on relation a=-3 v² m/s² where v in m/s. If it moves along a straight line and has velocity 10 m/s and position s = 8m when t=0, determine its velocity and position when t= 3 s. Where the velocity become zero. Discuss briefly.​

Answer 1

Step-by-step explanation:

Given: a = -3v^2

By definition, the acceleration is the time derivative of velocity v:

`a = (dv)/(dt) = - 3 {v}^(2)`

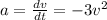
Re-arranging the expression above, we get

`\frac{dv}{ {v}^(2) } = - 3dt`

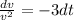
Integrating this expression, we get

`\int \frac{dv}{ {v}^(2) } = \int {v}^( - 2)dv = - 3\int dt`

`- (1)/(v) = - 3t + k`

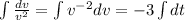
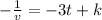
Since v = 10 when t = 0, that gives us k = -1/10. The expression for v can then be written as

`- (1)/(v) = - 3t - (1)/(10) = - ( (30 + 1)/(10) )`

or

`v = (10)/(30t +1 )`

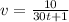
We also know that

`v = (ds)/(dt)`

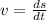
or

`ds = vdt = (10 \: dt)/(30t + 1)`

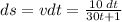
We can integrate this to get s:

`s = \int v \: dt = \int ( (10)/(30t + 1)) \: dt = 10 \int (dt)/(30t + 1)`

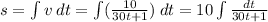
Let u = 30t +1

du = 30dt

so

`\int (dt)/(30t + 1) = (1)/(30) \int (du)/(u) = (1)/(30)\ln |u| + k`

`= (1)/(30)\ln |30t + 1| + k`

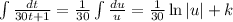
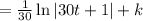
So we can now write s as

`s = (1)/(3)\ln |30t + 1| + k`

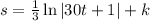
We know that when t = 0, s = 8 m, therefore k = 8 m.

`s = (1)/(3)\ln |30t + 1| + 8`

Next, we need to find the position and velocity at t = 3 s. At t = 3 s,

`v = (10)/(30(3) +1 ) = (10)/(91)(m)/(s) = 0.11 \: (m)/(s)`

`s = (1)/(3)\ln |30(3) + 1| + 8 = 9.5 \: m`

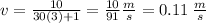
Note: velocity approaches zero as t -->
`\infty`