Question

if the angle of elevation of the sun is 40 degrees, and is decreasing 1/3 radians/hour how fast is the shadow of a 35m tall pole lengthening?

Answer 1

`(dx)/(dt) = 28.2 \: (m)/(hr)`

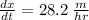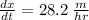
Explanation:

Let y = height of the pole = 35 m (constant)

x = length of the shadow

They are related as

`\tan \theta = (y)/(x)`

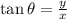
or

`x = (y)/( \tan\theta ) = y \cot \theta`

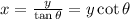
Taking the time derivative of the above expression and keeping in mind that y is constant, we get

`(dx)/(dt) = y( - \csc^(2) \theta) (d \theta)/(dt)`

Before we plug in the numbers, let's convert the degree unit into radians:

`40° * ( (\pi \: rad)/(180°)) = (2\pi)/(9) \: radians`

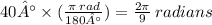
Since the angle is decreasing, then d(theta)/dt is negative. Therefore, the rate at which the shadow is lengthening is

`(dx)/(dt) = (35 \: m)( - \csc^(2) (2\pi)/(9) )( - (1)/(3) (rad)/(hr) )`

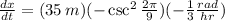
or

`(dx)/(dt) = 28.2 \: (m)/(hr)`